

Percents
Sommaire
débutant - This article is part of a series.

L’utilisation des pourcentiles est essentielle #
L’évaluation de l’expérience utilisateur (UX) est un aspect fondamental dans la développement des applications web. Pour comparer différentes ensembles de données UX, il est courant d’utiliser des mesures statistiques. L’average est une mesure populaire pour décrire le performance d’un ensemble de utilisateurs, mais utiliser seulement l’average peut être trompeur et ne représente pas suffisamment la qualité globale de l’expérience utilisateur. C’est pourquoi l’utilisation des percentiles est essentielle.
Qu’est-ce qu’un pourcentage ? #
Un pourcentage est une mesure statistique qui indique le niveau de données inférieurs à laquelle un certain pourcentage des données dans un ensemble ordonné se trouve. Par exemple, si le 50e pourcentage est de 20, cela signifie que 50% des données dans le lot sont inférieures à 20. Pour calculer un pourcentage, d’abord les données sont ordonnées du plus petit au plus grand. Ensuite, la valeur spécifique de données étant recherchée est identifiée. Par exemple, si l’on veut trouver le 25e pourcentage, on cherche la valeur inférieure à laquelle se trouve la moitié des données dans le lot.
Une fois que vous avez identifié le pourcentage souhaité, la formule suivante est utilisée pour calculer le pourcentage :
\(P = \dfrac{(n+1)*x}{100}\)
p est l’index de la percentile n est le nombre total de données dans le lot x est la pourcentage de données que vous voulez calculer
Après avoir calculé l’indice de perte centrale, la valeur correspondante est trouvée dans le tableau ordonné. Si l’indice de perte centrale est un entier, la valeur correspond à cette position directement. Si l’indice de perte centrale est une fraction numérique, il est interpolé linéairement entre les deux valeurs les plus proches du tableau ordonné.
Pour calculer le quartile à 25% dans un ensemble trié de données suivant :
10, 15, 20, 25, 30, 35, 40
D’abord, déterminer l’index de la percentile.
\(P = \dfrac{(7+1)*25}{100} = 2\)
Le valeur correspondante est la deuxième valeur dans le jeu de données, qui est 15. Par conséquent, le pourcentage à 25e est 15.
Comparaison Parallèle : Moyenne vs. Percentsiles
Assume a survey is carried out to assess user satisfaction on an online platform. Participants are requested to rate their experience on a scale from 1 to 10. The data collected is as follows:
| User | Rating |
|---|---|
| 1 | 6 |
| 2 | 7 |
| 3 | 8 |
| 4 | 9 |
| 5 | 10 |
Si l’on utilise la moyenne pour décrire l’expérience utilisateur, on obtient un score de 7,8. Cependant, si l’on examine les percentiles, on constate que 80 % des utilisateurs ont attribué une note de 8 ou plus à leur expérience. Cela suggère que la plupart des utilisateurs ont eu une expérience positive sur le site web. En revanche, l’utilisation de la moyenne pourrait masquer le fait que certains utilisateurs ont eu une expérience négative et d’autres une expérience exceptionnelle.
Exemples et Graphiques #
Veuillez examiner un autre exemple. Supposons que nous mesurons le temps nécessaire aux utilisateurs pour terminer une tâche dans un application. Les résultats obtenus sont les suivants :
| User | Time (seconds) |
|---|---|
| 1 | 10 |
| 2 | 15 |
| 3 | 20 |
| 4 | 20 |
| 5 | 30 |
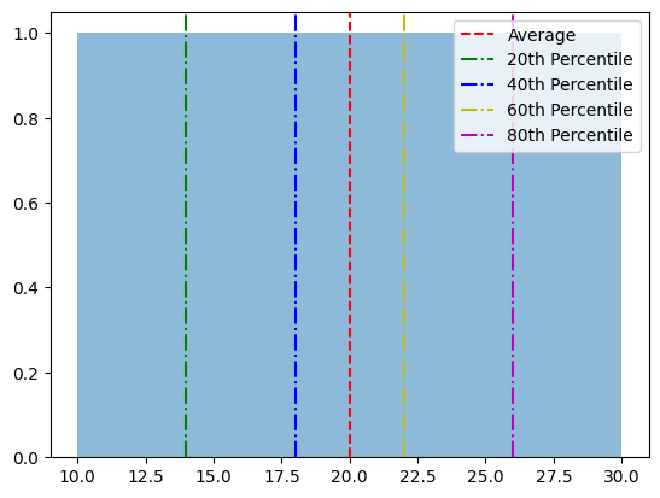
Si l’average est utilisé, il y aurait une moyenne de temps de 20 secondes. Cependant, si les percentiles sont observés, cela peut être vu que 80% des utilisateurs ont terminé le tâche en moins de 25 secondes. Ceci suggère que la plupart des utilisateurs trouvèrent facilement la tâche à accomplir dans un temps relativement court.
Dans le graphe suivant, il existe une différence entre l’utilisation du moyenne et des percentiles dans cet exemple:
Plugin de JMeter #
Le JMeter fournit un plugin qui graphique les pourcentiles des résultats d’une épreuve de performances.
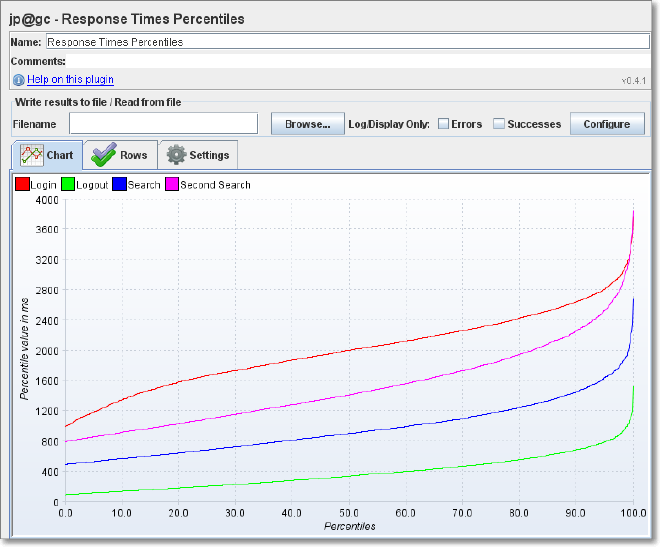
Vous pouvez trouver plus d’informations sur ce plugin à cette adresse:
Times de réponse pour les plugins JMeter
Conclusion #
En conclusion, l’utilisation des pourcentiles est essentielle pour une évaluation précise du bien-être utilisateur. Les pourcentiles fournissent des informations supplémentaires que la moyenne ne peut pas montrer. En analysant les pourcentiles, on obtient un aperçu plus complet de l’expérience utilisateur général et non seulement d’une mesure centrée. Pour obtenir une évaluation précise du bien-être utilisateur, l’utilisation des pourcentiles est essentielle.