

Percentiles
Tabla de contenido
Principiante - This article is part of a series.

El uso de percentiles es imprescindible #
La evaluación de la experiencia del usuario (UX) es un aspecto fundamental en el desarrollo de aplicaciones web. Para comparar diferentes conjuntos de datos de UX, es común utilizar medidas estadísticas. El promedio es una medida popular para describir el rendimiento de un conjunto de usuarios, pero el uso exclusivo del promedio puede ser engañoso y no representar adecuadamente la experiencia del usuario en general. Es por eso que el uso de percentiles es esencial.
¿ Qué es un Percentil ? #
Un percentil es una medida estadística que indica el valor por debajo del cual cae un porcentaje específico de datos en un conjunto de datos ordenados de menor a mayor. Por ejemplo, si el percentil 50 es 20, esto significa que el 50% de los datos en el conjunto están por debajo de 20. Para calcular un percentil, primero se ordenan los datos de menor a mayor. Luego, se identifica el porcentaje específico de datos que se desea calcular. Por ejemplo, si se desea calcular el percentil 25, esto significa que se está buscando el valor por debajo del cual se encuentra el 25% de los datos en el conjunto.
Una vez que se ha identificado el porcentaje deseado, se utiliza la siguiente fórmula para calcular el percentil:
\(P = \dfrac{(n+1)*x}{100}\)
- P es el índice del percentil
- n es el número total de datos en el conjunto
- x es el porcentaje de datos que se desea calcular
Después de calcular el índice del percentil, se encuentra el valor correspondiente en el conjunto de datos ordenados. Si el índice del percentil es un número entero, el valor correspondiente es simplemente el valor en esa posición. Si el índice del percentil es un número decimal, se interpola linealmente entre los dos valores más cercanos en el conjunto de datos ordenados.
Por ejemplo, para calcular el percentil 25 en un conjunto de datos ordenados de la siguiente manera:
10, 15, 20, 25, 30, 35, 40
Primero, se encuentra el índice del percentil:
\(P = \dfrac{(7+1)*25}{100} = 2\)
El valor correspondiente es el segundo valor en el conjunto de datos, que es 15. Por lo tanto, el percentil 25 es 15.
Comparación de lado a lado: promedio vs. percentiles #
Supongamos que se realiza una encuesta para evaluar la satisfacción de los usuarios de un sitio web. Se les pide que califiquen su experiencia en una escala del 1 al 10. Los resultados obtenidos son los siguientes:
| Usuario | Calification |
|---|---|
| 1 | 6 |
| 2 | 7 |
| 3 | 8 |
| 4 | 9 |
| 5 | 10 |
Si usamos el promedio para describir la experiencia de usuario, tendríamos que el puntaje promedio es de 7.8. Sin embargo, si observamos los percentiles, podemos ver que el 80% de los usuarios calificó su experiencia como un 8 o más alto. Esto sugiere que la mayoría de los usuarios tuvo una experiencia positiva en el sitio web. Por otro lado, si se usa el promedio, se puede ocultar el hecho de que algunos usuarios tuvieron una experiencia negativa y otros una experiencia excepcional.
Ejemplos y gráficos #
Veamos otro ejemplo. Supongamos que se está midiendo el tiempo que toma a los usuarios realizar una tarea en una aplicación. Los resultados obtenidos son los siguientes:
| Usuario | Tiempo (segundos) |
|---|---|
| 1 | 10 |
| 2 | 15 |
| 3 | 20 |
| 4 | 20 |
| 5 | 30 |
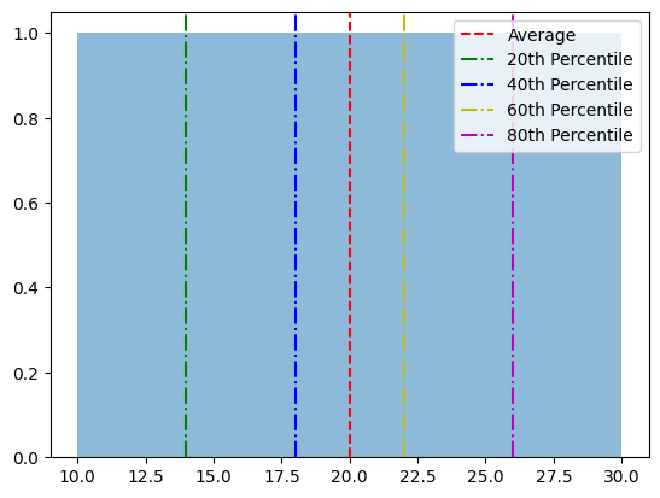
Si se usa el promedio, se tendría un tiempo promedio de 20 segundos. Pero si se observan los percentiles, se puede ver que el 80% de los usuarios completó la tarea en 25 segundos o menos. Esto sugiere que la mayoría de los usuarios encontró la tarea fácil de completar en poco tiempo.
En la siguiente gráfica se muestra la diferencia entre el uso del promedio y los percentiles en este ejemplo:
JMeter Plugin #
JMeter proveed un plugin que grafíca los percentiles de los resultados de una prueba de performance.
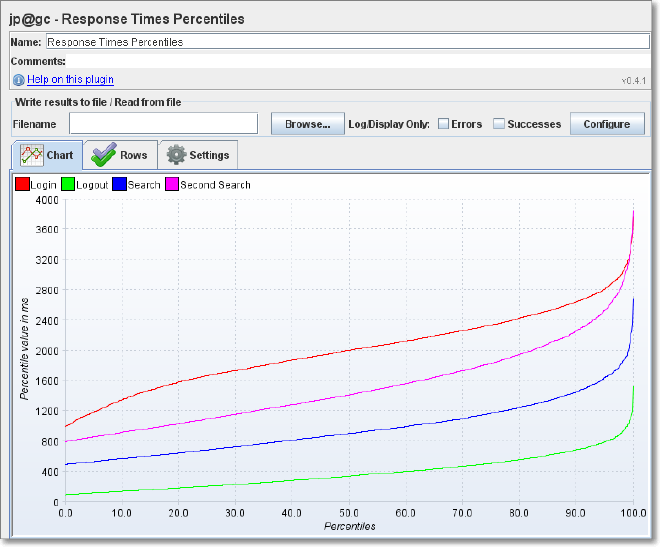
Puedes encontras mas información acerca de este plugin en este link:
Response Times Percentiles -JMeter-Plugins.org
Conclusión #
En conclusión, el uso de percentiles es imprescindible para una evaluación precisa de la experiencia de usuario. Los percentiles proporcionan información adicional que el promedio no puede mostrar. Al analizar los percentiles, se puede obtener una imagen más completa de la experiencia del usuario en general, y no solo una medida de tendencia central. Si se desea obtener una evaluación precisa de la experiencia de usuario, el uso de percentiles es imprescindible.